| 时代TH200数显A型邵氏硬度计 |
| 时代THBRV-187.5D/THBRVP-187.5E电动(数显 |
| 时代THB-3000E/THBS-3000E/THBS-3000DB直读 |
| THBP-62.5数显小负荷布氏硬度计 |
| TMVP-1/TMVP-1S大屏数显自动(手动)转 |
| 时代TMVM-1触摸屏显微维氏硬度计 |
正弦信号真有效值--测振仪系列知识讲座五
什么是机械振动正弦信号的真有效值--测振仪系列知识讲座五
所谓的“真有效值”是“真正的有效值”之意,英文缩写为:TRMS,亦称“真均方根值”,即如式(2-10)、(2-11)所示。
而式(2-11)的近似公式为:
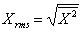 (2-12)
(2-12)
式中:
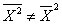
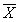 ——在0~T周期内所有时刻(t =1、2、3、…、n)读数的平均值,即:
——在0~T周期内所有时刻(t =1、2、3、…、n)读数的平均值,即: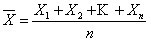 ;
;
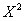 ——在0~T周期内,每一时刻的读数值(例如:t=1 时刻的值=
——在0~T周期内,每一时刻的读数值(例如:t=1 时刻的值= 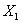 )
)
减去“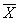 ”值之后的平方和即:
”值之后的平方和即:
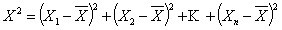
 上面的“—”——即为平均值之意,它表示为:
上面的“—”——即为平均值之意,它表示为: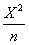 。
。
利用式(2-12)借助于电路,对简谐振动信号X(t)进行“平方——取平均值——开平方”运算,就获得该信号的有效值。因为该信号的有效值是由有效值定义式[ 式(2-11)、(2-12)]求出的,故称之为真有效值。
若将式(2-12)两边平方,且设: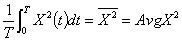 ,就可以得到真有效值的另一种表达方式:
,就可以得到真有效值的另一种表达方式:
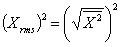 即:
即:
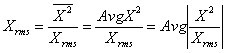 (2-13)
(2-13)
式中,Avg 表示取平均值。借助于电路,对简谐振动信号X(t) 进行“取绝对值——平方╱除法——取平均值”运算,也能得到该信号的真有效值。
由于同时完成“X2╱Xrms”两步运算,与公式(2-12)分步运算相比,电路运算的动态范围大为减小,既便于电路设计,又保证了仪器准确度的指标。因此,式(2-13)的原理被普遍采用。真有效值仪器的核心是TRMS╱DC转换器,这类电路已实现单片集成化,其准确度可达≤±0.2%。
而普通的数字显示仪器的有效值均由平均值响应的AC╱DC转换器运算而获得的,它是由运算放大器和二极管组成的半波(或全波)线性整流电路来完成有效值的运算的。其具有线性度好、准确度高、电路简单、成本低廉等优点。由于它是按照正弦波平均值与有效值的关系而定义的[请详见式(3-4)所述],因此所构成的仪器仅适合于测量不失真的正弦波(简谐振动)信号数据,由于常测信号均非都是不失真的正弦波(简谐振动)信号,其测量误差相对于具有真有效值功能的仪器来讲,最大竟达99%。表2-1即为此两种仪器的测量误差比较。
表2-1 两种仪器的测量误差比较
|
被测波形 |
峰值 指标 Cf |
波形 指标 Sf |
真有效值 Xrms |
平均值 (或绝对 平均值)①
|
平均值 仪器读数②
|
平均值 仪器 相对误差 % |
|
|
不失真正弦 (简谐)波 |
1.414 |
1.111 |
0.707Xmax |
0.636Xmax |
0.707Xmax |
0 |
|
|
半波整流 |
2 |
1.571 |
0.5 Xmax |
0.318Xmax |
0.353Xmax |
-29.9 |
|
|
方波 |
1 |
1 |
Xmax |
Xmax |
1.111Xmax |
+11.1 |
|
|
矩形波 |
佔空比 50% |
2
10 |
2
10 |
0.5Xmax
0.1Xmax |
0.25Xmax
0.01Xmax |
0.277Xmax
0.01Xmax |
-44.6
-99 |
|
佔空比 25% |
|||||||
|
三角波 |
1.732 |
1.155 |
0.577Xmax |
0.5Xmax |
0.555Xmax |
-3.8 |
|
|
锯齿波 |
1.155 |
1.155 |
0.577Xmax |
0.5Xmax |
0.555Xmax |
-3.8 |
|
②——平均值仪器的读数等于1.111 乘以平均值(或绝对平均值)。1.111 也称之为仪器的标定系数。
注:测振仪系列知识讲座为连载文章,欢迎大家继续关注。www.101718.com/tech/cezhenyi/435.html
阅读本文的用户还对以下文章感兴趣:
信号频域分析方法--测振仪系列知识讲座九
机械振动信号分类--测振仪系列知识讲座二
测振仪原理及使用